Self-organizing map
A self-organizing map (SOM) or self-organizing feature map (SOFM) is a type of artificial neural network that is trained using unsupervised learning to produce a low-dimensional (typically two-dimensional), discretized representation of the input space of the training samples, called a map. Self-organizing maps are different from other artificial neural networks in the sense that they use a neighborhood function to preserve the topological properties of the input space.
This makes SOMs useful for visualizing low-dimensional views of high-dimensional data, akin to multidimensional scaling. The model was first described as an artificial neural network by the Finnish professor Teuvo Kohonen, and is sometimes called a Kohonen map.[1]
Like most artificial neural networks, SOMs operate in two modes: training and mapping. Training builds the map using input examples. It is a competitive process, also called vector quantization. Mapping automatically classifies a new input vector.
A self-organizing map consists of components called nodes or neurons. Associated with each node is a weight vector of the same dimension as the input data vectors and a position in the map space. The usual arrangement of nodes is a regular spacing in a hexagonal or rectangular grid. The self-organizing map describes a mapping from a higher dimensional input space to a lower dimensional map space. The procedure for placing a vector from data space onto the map is to first find the node with the closest weight vector to the vector taken from data space. Once the closest node is located it is assigned the values from the vector taken from the data space.
While it is typical to consider this type of network structure as related to feedforward networks where the nodes are visualized as being attached, this type of architecture is fundamentally different in arrangement and motivation.
Useful extensions include using toroidal grids where opposite edges are connected and using large numbers of nodes. It has been shown that while self-organizing maps with a small number of nodes behave in a way that is similar to K-means, larger self-organizing maps rearrange data in a way that is fundamentally topological in character.
It is also common to use the U-Matrix. The U-Matrix value of a particular node is the average distance between the node and its closest neighbors (ref. 9). In a square grid for instance, we might consider the closest 4 or 8 nodes (the Von Neumann neighborhood and Moore neighborhood respectively), or six nodes in a hexagonal grid.
Large SOMs display properties which are emergent. In maps consisting of thousands of nodes, it is possible to perform cluster operations on the map itself.[2]
Contents |
Learning algorithm
The goal of learning in the self-organizing map is to cause different parts of the network to respond similarly to certain input patterns. This is partly motivated by how visual, auditory or other sensory information is handled in separate parts of the cerebral cortex in the human brain.[3]
The weights of the neurons are initialized either to small random values or sampled evenly from the subspace spanned by the two largest principal component eigenvectors. With the latter alternative, learning is much faster because the initial weights already give good approximation of SOM weights.[4]
The network must be fed a large number of example vectors that represent, as close as possible, the kinds of vectors expected during mapping. The examples are usually administered several times as iterations.
The training utilizes competitive learning. When a training example is fed to the network, its Euclidean distance to all weight vectors is computed. The neuron with weight vector most similar to the input is called the best matching unit (BMU). The weights of the BMU and neurons close to it in the SOM lattice are adjusted towards the input vector. The magnitude of the change decreases with time and with distance from the BMU. The update formula for a neuron with weight vector Wv(t) is
- Wv(t + 1) = Wv(t) + Θ (v, t) α(t)(D(t) - Wv(t)),
where α(t) is a monotonically decreasing learning coefficient and D(t) is the input vector. The neighborhood function Θ (v, t) depends on the lattice distance between the BMU and neuron v. In the simplest form it is one for all neurons close enough to BMU and zero for others, but a Gaussian function is a common choice, too. Regardless of the functional form, the neighborhood function shrinks with time.[3] At the beginning when the neighborhood is broad, the self-organizing takes place on the global scale. When the neighborhood has shrunk to just a couple of neurons the weights are converging to local estimates.
This process is repeated for each input vector for a (usually large) number of cycles λ. The network winds up associating output nodes with groups or patterns in the input data set. If these patterns can be named, the names can be attached to the associated nodes in the trained net.
During mapping, there will be one single winning neuron: the neuron whose weight vector lies closest to the input vector. This can be simply determined by calculating the Euclidean distance between input vector and weight vector.
While representing input data as vectors has been emphasized in this article, it should be noted that any kind of object which can be represented digitally and which has an appropriate distance measure associated with it and in which the necessary operations for training are possible can be used to construct a self-organizing map. This includes matrices, continuous functions or even other self-organizing maps.
Preliminary definitions
Consider a n×m array of nodes each of which contains a weight vector and is aware of its location in the array. Each weight vector is of the same dimension as the node's input vector. The weights may initially be set to random values.
Now we need input to feed the map. (The generated map and the given input exist in separate subspaces.) We will create three vectors to represent colors. Colors can be represented by their red, green, and blue components. Consequently our input vectors will have three components, each corresponding to a color space. The input vectors will be:
- R = <255, 0, 0>
- G = <0, 255, 0>
- B = <0, 0, 255>
The color training vector data sets used in SOM:
- threeColors = [255, 0, 0], [0, 255, 0], [0, 0, 255]
- eightColors = [0, 0, 0], [255, 0, 0], [0, 255, 0], [0, 0, 255], [255, 255, 0], [0, 255, 255], [255, 0, 255], [255, 255, 255]
The data vectors should preferably be normalized (vector length is equal to one) before training the SOM.
Neurons (40 x 40 square grid) are trained for 250 iterations with a learning rate of 0.1 using the normalized Iris flower data set which has four dimensional data vectors. A color image formed by first three dimensions of the four dimensional SOM weight vectors (top left), pseudo-color image of the magnitude of the SOM weight vectors (top right), U-Matrix (Euclidean distance between weight vectors of neighboring cells) of the SOM (bottom left) and overlay of data points (red: I. setosa, green: I. versicolor and blue: I. verginica) on the U-Matrix based on the minimum Euclidean distance between data vectors and SOM weight vectors (bottom right).
Variables
These are the variables needed, with vectors in bold,
 denotes current iteration
denotes current iteration is the limit on time iteration
is the limit on time iteration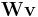 is the current weight vector
is the current weight vector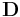 is the target input
is the target input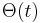 is restraint due to distance from BMU, usually called the neighborhood function, and
is restraint due to distance from BMU, usually called the neighborhood function, and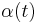 is learning restraint due to time.
is learning restraint due to time.
Algorithm
- Randomize the map's nodes' weight vectors
- Grab an input vector
- Traverse each node in the map
- Use Euclidean distance formula to find similarity between the input vector and the map's node's weight vector
- Track the node that produces the smallest distance (this node is the best matching unit, BMU)
- Update the nodes in the neighborhood of BMU by pulling them closer to the input vector
- Wv(t + 1) = Wv(t) + Θ(t)α(t)(D(t) - Wv(t))
- Increase t and repeat from 2 while
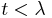
Interpretation
There are two ways to interpret a SOM. Because in the training phase weights of the whole neighborhood are moved in the same direction, similar items tend to excite adjacent neurons. Therefore, SOM forms a semantic map where similar samples are mapped close together and dissimilar apart. This may be visualized by a U-Matrix (Euclidean distance between weight vectors of neighboring cells) of the SOM.[5]
The other way is to think of neuronal weights as pointers to the input space. They form a discrete approximation of the distribution of training samples. More neurons point to regions with high training sample concentration and fewer where the samples are scarce.
SOM may be considered a nonlinear generalization of Principal components analysis (PCA).[6] It has been shown, using both artificial and real geophysical data, that SOM has many advantages[7][8] over the conventional feature extraction methods such as Empirical Orthogonal Functions (EOF) or PCA.
Originally, SOM was not formulated as a solution to an optimisation problem. Nevertheless, there have been several attempts to modify the definition of SOM and to formulate an optimisation problem which gives similar results.[9] For example, Elastic maps use for approximation of principal manifolds[10] the mechanical metaphor of elasticity and analogy of the map with elastic membrane and plate.
Alternatives
- The generative topographic map (GTM) is a potential alternative to SOMs. In the sense that a GTM explicitly requires a smooth and continuous mapping from the input space to the map space, it is topology preserving. However, in a practical sense, this measure of topological preservation is lacking.[11]
- The time adaptive self-organizing map (TASOM) network is an extension of the basic SOM. The TASOM employs adaptive learning rates and neighborhood functions. It also includes a scaling parameter to make the network invariant to scaling, translation and rotation of the input space. The TASOM and its variants have been used in several applications including adaptive clustering, multilevel thresholding, input space approximation, and active contour modeling.[12]. Moreover, a Binary Tree TASOM or BTASOM, resembling a binary natural tree having nodes composed of TASOM networks has been proposed where the number of its levels and the number of its nodes are adaptive with its environment.[13]
- The growing self-organizing map (GSOM) is a growing variant of the self-organizing map. The GSOM was developed to address the issue of identifying a suitable map size in the SOM. It starts with a minimal number of nodes (usually four) and grows new nodes on the boundary based on a heuristic. By using a value called the spread factor, the data analyst has the ability to control the growth of the GSOM.
See also
- Neural gas
- Large Memory Storage and Retrieval (LAMSTAR) neural networks:
Large Memory Storage and Retrieval (LAMSTAR) neural networks are SOM-based neural networks that can employ a very large number of SOM layers of differing number of neurons to store the LAMSTAR's input sub-words of an input word. The LAMSTAR also employs one or more output (decision) SOM layers and a multitude of link-weights connecting the winning neurons of the various input layers to the decision layers. The link-weights from all winning input layers to a given output lay SOM module are summed. The winning decision is that with the highest link-weight total. Initial weights are all set to zero. The network is fully transparent since the link-weights give the relative significance of a given input layer (sub-word) or even of any input neuron, relative to a given decision. The Lamstar has a forgetting capability, subject to a pre-assigned forgetting factor. Weights are continuously learnt (updated) by punishments and rewards that are added/subtracted to/from each link weight of any winning input neuron after each run or iteration of the input data. The network was developed by Daniel Graupe, Hubert Kordylewsky and Nathan Schneider. See: D Graupe, Principles of Artificial Neural Networks, 2nd edition, World Scientific Publishers, 2007. The LAMSTAR has been used in many applications involving large and diverse data sets ranging from medical diagnosis, economics, finance, cyber security and beyond,
- Hybrid Kohonen SOM
A special type of Kohonen SOM is the Hybrid Kohonen Self Organizing Map where the network architecture consists of an input layer fully connected to a 2–D SOM or Kohonen layer. The output from the Kohonen layer, which is the winning neuron feeds into a hidden layer and finally into an output layer. In other words, the Kohonen SOM is the front–end, while the hidden and output layer of a MLP is the back–end of the Hybrid Kohonen SOM. The Hybrid Kohonen SOM was first applied to machine vision systems for image classification and recognition. See: F. Nabhani and T. Shaw. Performance analysis and optimisation of shape recognition and classification using ANN. Robotics and Computer Integrated Manufacturing, 18:177–185, 2002. Hybrid Kohonen SOM has been used in weather prediction and especially in forecasting stock prices, which has made such a challenging task considerably easier. It is fast and efficient with less classification error, hence, a better predictor compared to Kohonen SOM and Backpropagation networks. [14]
References
- ^ Kohonen, T. and Honkela, T. (2007). "Kohonen network". Scholarpedia. http://www.scholarpedia.org/article/Kohonen_network.
- ^ Ultsch, Alfred (2007). Emergence in Self-Organizing Feature Maps, In Proceedings Workshop on Self-Organizing Maps (WSOM '07). Bielefeld, Germany. ISBN 978-3-00-022473-7.
- ^ a b Haykin, Simon (1999). "9. Self-organizing maps". Neural networks - A comprehensive foundation (2nd ed.). Prentice-Hall. ISBN 0-13-908385-5.
- ^ "Intro to SOM by Teuvo Kohonen". SOM Toolbox. http://www.cis.hut.fi/projects/somtoolbox/theory/somalgorithm.shtml. Retrieved 2006-06-18.
- ^ Ultsch A (2003). U*-Matrix: a tool to visualize clusters in high dimensional data. University of Marburg, Department of Computer Science, Technical Report Nr. 36:1-12.
- ^ Yin H. Learning Nonlinear Principal Manifolds by Self-Organising Maps, In: Gorban A. N. et al. (Eds.), LNCSE 58, Springer, 2007 ISBN 978-3-540-73749-0
- ^ Liu, Y., and R.H. Weisberg (2005), Patterns of ocean current variability on the West Florida Shelf using the self-organizing map. Journal of Geophysical Research, 110, C06003, doi:10.1029/2004JC002786.
- ^ Liu, Y., R.H. Weisberg, and C.N.K. Mooers (2006), Performance evaluation of the Self-Organizing Map for feature extraction. Journal of Geophysical Research, 111, C05018, doi:10.1029/2005jc003117.
- ^ T. Heskes, Energy functions for self-organizing maps, In: Kohonen Maps, E. Oja, S. Kaski (Eds.), Elsevier, 1999.
- ^ Gorban A.N., Kegl B., Wunsch D., Zinovyev A. (Eds.), Principal Manifolds for Data Visualisation and Dimension Reduction, LNCSE 58, Springer: Berlin – Heidelberg – New York, 2007. ISBN 978-3-540-73749-0
- ^ Kaski, S.. Data exploration using self-organizing maps, Acta Polytechnica Scandinavica, Mathematics, Computing and Management in Engineering Series No. 82, Espoo 1997, 57 pp..
- ^ Hamed Shah-Hosseini and Reza Safabakhsh. TASOM: A New Time Adaptive Self-Organizing Map, IEEE TRANSACTIONS ON SYSTEMS, MAN, AND CYBERNETICS—PART B: CYBERNETICS, VOL. 33, NO. 2, APRIL 2003, pp. 271-282.[1]
- ^ Hamed Shah-Hosseini. Binary tree time adaptive self-organizing map , Neurocomputing, Vol. 74, No. 11, May 2011, pp. 1823-1839.[2]
- ^ Mark O. Afolabi and Olatoyosi Olude (2007), Predicting Stock Prices Using a Hybrid Kohonen Self Organizing Map (SOM), in 40th Annual Hawaii International Conference On System Sciences’, 2007, IEEE, pp. 48–56.
External links
- Self-organizing maps for WEKA: Implementation of Self-organizing maps in Java, for the WEKA Machine Learning Workbench.
- Self-organizing maps for Ruby: Implementation of Self-organizing maps in Ruby, for the AI4R project.
- Spice-SOM: A free GUI application of Self-Organizing Map
- IFCSoft: An open-source Java platform for generating Self-Organizing Maps